頻度分布・偏差・分散

4.2. 頻度分布・偏差・分散#

全体の様子、ばらつきの広がり具合など全体をながめわたすための考え方です。

ここからはつぎのcellでつくる df_new を使って、頻度分布、四方位範囲、分散、標準偏差についてPythonで確認します。

import random
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
%matplotlib inline

df_new = pd.DataFrame({'cc':[random.normalvariate(100,25) for x in range(200)],
                      'item':[['water','wine','oil','juice','milk'][random.randrange(5)] for x in range(200)]})
df_new.sample(3)

	cc	item
22	78.029004	milk
199	99.005910	wine
24	137.959509	milk

df_new.dtypes

cc      float64
item     object
dtype: object

df_new.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 200 entries, 0 to 199
Data columns (total 2 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   cc      200 non-null    float64
 1   item    200 non-null    object 
dtypes: float64(1), object(1)
memory usage: 3.3+ KB

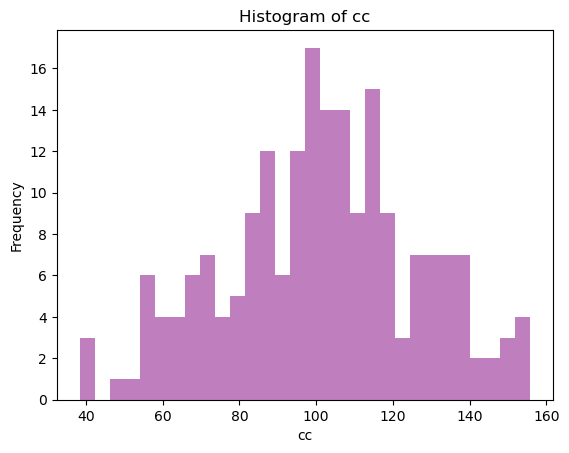
4.2.1. 頻度分布（histogram）#

それぞれの値の起こる頻度（回数）を数えたものです。

plt.hist()を使って頻度分布（Histogram）を描写します。ドキュメント

plt.hist(df_new['cc'], bins=30, color = 'purple', alpha = 0.5)
plt.title('Histogram of cc')
plt.xlabel('cc')
plt.ylabel('Frequency')
plt.show()

../../_images/7df332022632264e8083f2a1fa363a211e4becfb08e9bac3f6b05018936e602c.png

4.2.2. 四分位範囲#

データの散らばり方を直感的、視覚的に表そうとするもの。データ全体を大きさの順に並べて四等分してみせます。
大きさの順で小さい方から1/4のところの値を第一四分位数、2/4のところの値を第二四分位数、3/4のところを第三四分位数と呼びます。第二四分位数はちょうど中央値に一致します。
箱ひげ図を用いて描くことが多いです。

matplotlibのboxplotを用いて df_new の cc　列について箱ひげ図を描きます。

plt.figure(figsize=(5,5))
plt.boxplot(df_new['cc'],showmeans=True)
plt.title('BoxPlot of cc')
plt.grid() #　グリッド線を描きます
plt.ylabel('cc')
plt.show()

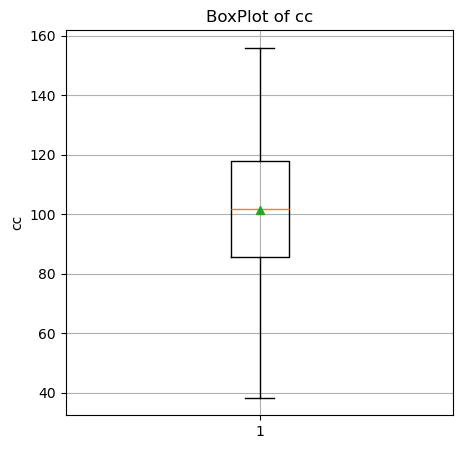
../../_images/712b08b57346e12b002ddac77dcd8b68ac33789c0e8b4def821c0aabb990a196.png

小さい方から、箱の下辺が第一四分位数、オレンジの水平線が第二四分位数、箱の上辺が第三四分位数を示しています。
ここでは、逆T字とT字の水平線はそれぞれウィンカの終わりの位置を示しています。

ウィンカの上限はとはここでは、

\[Q3 + whis*IQR\]

\[IQR = 第三四分位数(Q3) - 第一四分位数(Q1)\]

\[whis = 1.5(default値で変更可能)\]

下限は、\(Q1 - whis*IQR\)となります。このウィンカを超えると外れ値としてプロットされます。

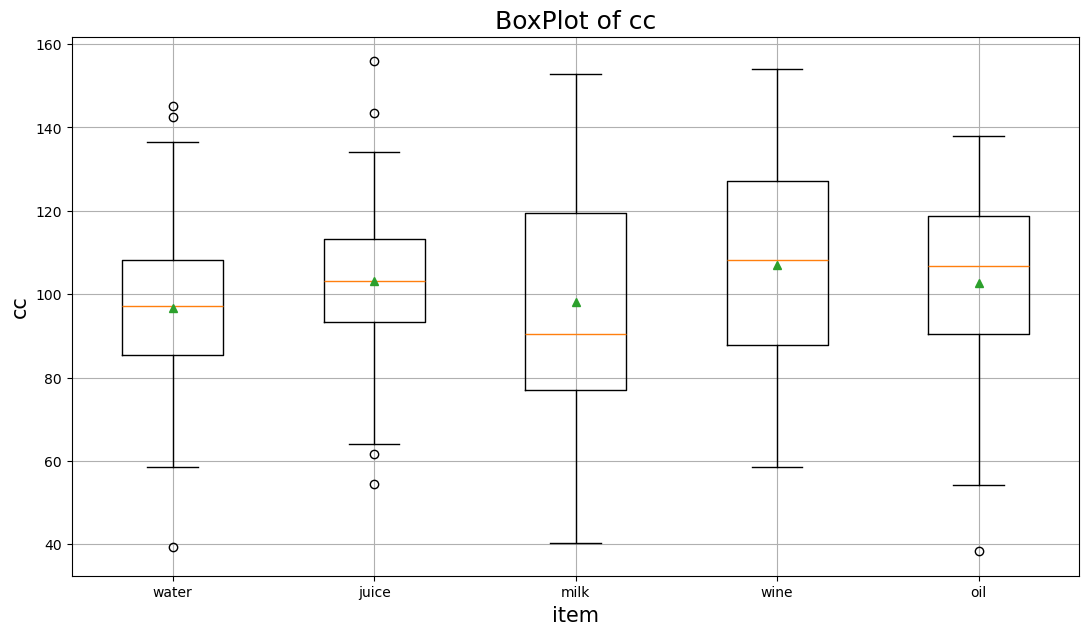
続いて、df_new の item　別の箱ひげ図を描いてみましょう。

plt.figure(figsize=(13,7))

data = [df_new.loc[df_new['item'].isin([x]),'cc'] for x in df_new['item'].unique()]

plt.boxplot(data, 
            labels = list(df_new['item'].unique()),
            showmeans=True)
plt.title('BoxPlot of cc', size=18)
plt.grid() 
plt.ylabel('cc',size=15)
plt.xlabel('item',size=15)
plt.yticks(size=10)
plt.xticks(size=10)
plt.show()

../../_images/4f7115b238c898f04fead4dc2e61dfa3e7449888e75ad74746cb678d8bd463e3.png

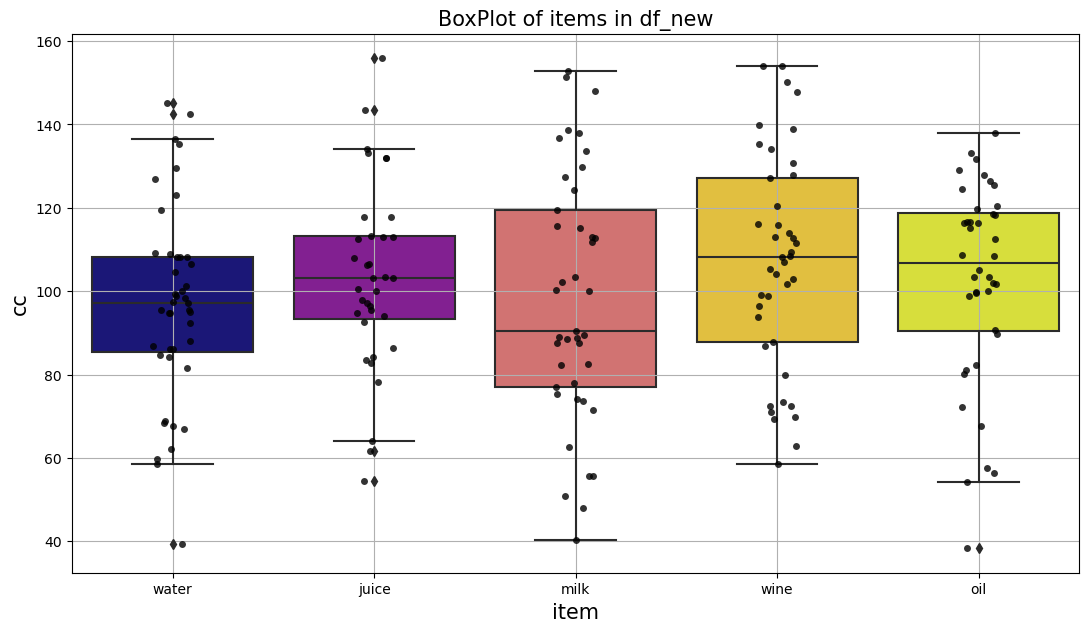
4.2.3. 参考 Stripplot#

上の例のように箱ひげ図はデータの散らばり方を直感的に捉え上で有用です。
しかし、それぞれのデータがどのような値を持っているかを把握することができないのが難点です。
seabornのstripplotを使って簡単に確認する方法があるので、紹介します。

palette = [plt.get_cmap('plasma')(i*0.3) for i in range(len(df_new['item'].unique()))]

plt.figure(figsize=(13,7))
sns.boxplot(x='item', y='cc', data=df_new, 
            palette = palette)
sns.stripplot(x='item', y='cc', data=df_new, jitter=True, color = 'black', alpha = 0.8)
plt.xlabel('item',fontsize=15)
plt.ylabel('cc',fontsize=15)
plt.yticks(fontsize=10)
plt.xticks(fontsize=10)
plt.title('BoxPlot of items in df_new', fontsize=15)
plt.grid()
plt.show()

/opt/anaconda3/lib/python3.11/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
  with pd.option_context('mode.use_inf_as_na', True):
/opt/anaconda3/lib/python3.11/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
  with pd.option_context('mode.use_inf_as_na', True):

../../_images/2b96830c4bac91c706a1cea20bf8919df7d58bf1a2654850ea1eae4f2f5f6834.png

4.2.4. 分散・標準偏差#

4.2.4.1. 分散（variance）#

データの散らばり具合を示す指標の１つ。１つ１つのデータ\(x_i\)と平均\(\bar{X}\) の差をの二乗の和をデータの個数で割った値です。個々のデータが平均値からどれだけ離れているのかの距離\((x_i-\bar{X})^2\)を二乗して合計し、データの個数で割ることで標準化した値です。

\[ s^2 = \frac{\sum_i(x_i-\bar{X})^2}{n} \]

4.2.4.2. 標準偏差（standard deviation）#

分散の平方根です

\[ \sigma = \sqrt{\frac{\sum_i(x_i-\bar{X})^2}{n}} \]

分散および標準偏差をnではなく n-1 で割って求める不偏分散(標本から母集団の分散の推定) などもあります。詳しくは統計関連の文献をご確認ください。

ここからdef_newを用いて分散と標準偏差を求めましょう。

df_newのcc列の分散と標準偏差を求めます。

df_new['cc'].var()

647.3149674242954

このvarはn-1で割った不偏分散を求めています。nで割った分散を求めるには、var(ddof=0)とします。

var() の公式ドキュメントも参照してください。

df_new['cc'].var(ddof=0)

644.078392587174

df_newのcc列の標準偏差を求めます。pandas のstdではdefault でn-1で割ったものとなっています。

df_new['cc'].std()

25.442385254222835

nで割った分散を求めるには、std(ddof=0)とします。

df_new['cc'].std(ddof=0)

25.37869958424139

4.2.5. まとめ#

ここでは、与えられたデータがどのようなものであるのかを概観するためのいくつかの方法について紹介しました。
pandasではdescribe()を使って基本的な統計量を一変に得ることができます。
なお、学術論文においては、標本数（n）、平均（mean）、標準偏差（std）、最小値（min）、最大値（max）を最低限の記述統計量として掲載することが基本となっています。

df_new.groupby(['item']).describe()

	cc
	count	mean	std	min	25%	50%	75%	max
item
juice	35.0	103.211522	22.315778	54.512716	93.323082	103.055338	113.162685	155.883490
milk	41.0	98.138842	29.942200	40.388166	76.957203	90.501855	119.462462	152.806575
oil	40.0	102.692130	24.118087	38.327415	90.390717	106.793141	118.766161	138.020927
water	43.0	96.772143	23.498995	39.395348	85.387574	97.213128	108.182378	145.074695
wine	41.0	106.927070	26.150360	58.572095	87.872449	108.236327	127.170841	154.077842

df_new.describe()

	cc
count	200.000000
mean	101.444965
std	25.442385
min	38.327415
25%	85.765790
50%	101.899483
75%	117.816992
max	155.883490