5.2. 回帰分析

5.2.1. 単回帰分析

ここではまず、説明変数が１つの単回帰（Simple Regression）を考えます。

\(y_i = \beta_0+\beta_1x_i+\epsilon_i\)

• \(y_i\)： 被説明変数（explained variable）, 従属変数（dependent variable）,アウトカム（outcome variable）など

• \(x_i\)： 説明変数（explanatory variable）, 独立変数（independent variable）など

• \(\epsilon_i\)： 誤差項（erros, error terms) 平均はゼロと仮定

• \(i\)： 観測値のインデックス

• \(\beta_0\)：定数項、切片パラメター

• \(\beta_1\)：係数パラメター、傾きパラメター

最小二乗法推定法（Ordinary Least Squares; OLS）やモーメント法、最尤法などで推定できます。

最小二乗法の場合は、

\(\sum_{i=1}^{n}(y_i-\beta_0-\beta_1x_i)^2\) を最小化する\(\beta_0\), \(\beta_1\)を求めます

推定した係数\(\beta_1\)は被説明変数\(y_i\)に対する説明変数\(x_i\)の影響度合いを表す限界効果、あるいは説明変数が１単位変化した場合の被説明変数の変化（\(\frac{\delta y_i}{\delta x_i}\)）と解釈することができます。

ここではstatsmodels を用いて単回帰分析を行います。

statsmodelsは線形回帰、一般化線形モデル、制限付き従属変数モデル、ARIMA、VARモデルなどをカバーするパッケージです。

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt

回帰分析で用いるデータを読み込みます。

ここでは、statsmodelsに付属するstatecrimeというデータセットの1つで、1996年American National Elections Studyのデータを用いて回帰分析を行います。

data = sm.datasets.statecrime.load_pandas().data

# dataの最初の2行を表示
data.head(2)

	violent	murder	hs_grad	poverty	single	white	urban
state
Alabama	459.9	7.1	82.1	17.5	29.0	70.0	48.65
Alaska	632.6	3.2	91.4	9.0	25.5	68.3	44.46

このデータは以下のデータを格納しています

• state: 州の名前

• violent: 暴力犯罪発生率／人口10万人。殺人を含む

• murder: 殺人事件の発生率／人口10万人

• hs_grad: 高等学校以上を卒業した人口の割合

• poverty: 貧困線以下の人口の割合

• white: 白人のみの人口の割合

• single: 片親のいる家族世帯の割合

• urban: 市街化区域に住む人口の割合

murder 殺人事件の発生率を被説明変数(\(y_i\))、poverty貧困人口の割合を説明変数(\(x_i\))とした単回帰分析を行います。

mod = sm.OLS.from_formula('murder ~ poverty', data = data)
res = mod.fit()
print(res.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                 murder   R-squared:                       0.294
Model:                            OLS   Adj. R-squared:                  0.279
Method:                 Least Squares   F-statistic:                     20.36
Date:                Mon, 30 Dec 2024   Prob (F-statistic):           4.03e-05
Time:                        08:24:47   Log-Likelihood:                -128.98
No. Observations:                  51   AIC:                             262.0
Df Residuals:                      49   BIC:                             265.8
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     -3.8989      1.998     -1.952      0.057      -7.913       0.115
poverty        0.6351      0.141      4.512      0.000       0.352       0.918
==============================================================================
Omnibus:                       63.810   Durbin-Watson:                   2.087
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              533.355
Skew:                           3.237   Prob(JB):                    1.53e-116
Kurtosis:                      17.459   Cond. No.                         65.7
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

** その他の結果の表の読み方はこのページを参照してください。

\(\beta_0\)の推計値はintercept行、coef列の値-3.8989です。 \(\beta_1\)の推計値はpoverty行、coef列の値0.6351です。 すなわち、\(\beta_1\)は貧困人口の割合が1ポイント高い場合、殺人事件発生率は何ポイント変化するかを示しています。 今回の単回帰分析推定結果からは貧困人口の割合が1ポイント高い場合、殺人事件発生率は約0.6ポイント高いことを示しています。

また、回帰モデルの当てはまりの良さは自由度調整済決定係数Adj. R-squaredで確認できます。 0から1までの間の値で、値が大きいほど回帰直線がデータをうまく説明できている（フィットしている）ことになります。

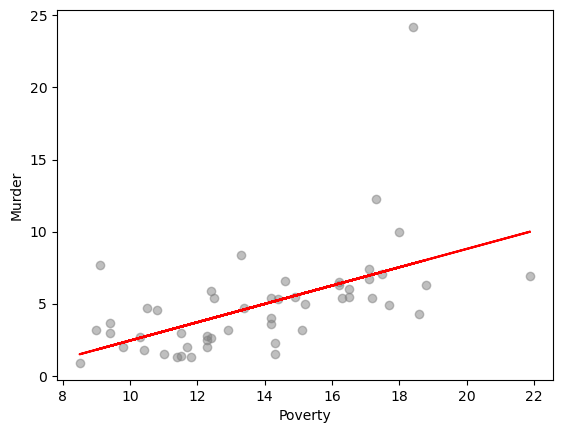
回帰分析の結果を図で確認します。

\(\hat{y}\)予測値を取得し、その上で回帰直線を示します。

y = data['murder']
x = data['poverty']
y_hat = res.fittedvalues
plt.scatter(x=x, y=y, color = 'grey', alpha= .5)
plt.plot(x, y_hat, color = 'red')
plt.xlabel('Poverty')
plt.ylabel('Murder')
plt.show()

最小二乗法のイメージを図で掴んでみます。

for i in range(len(y)):
    dot_fitted_values = [x[i], x[i]]
    dot_org_values = [y[i], y_hat[i]]
    plt.plot(dot_fitted_values, dot_org_values, linestyle='--', 
             color='grey',alpha=0.5)
plt.scatter(x=x, y=y, color = 'grey', alpha= .5)
plt.plot(x, y_hat, color = 'red')
plt.xlabel('Poverty')
plt.ylabel('Murder')
plt.title(r'$\hat Y = {:.2f}+{:.2f}X$'.format(res.params[0], res.params[1]))
plt.show()

/var/folders/z5/0lnyp_m54dqc1xkz22ncbj2h0000gn/T/ipykernel_22931/4200653138.py:2: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
  dot_fitted_values = [x[i], x[i]]
/var/folders/z5/0lnyp_m54dqc1xkz22ncbj2h0000gn/T/ipykernel_22931/4200653138.py:3: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
  dot_org_values = [y[i], y_hat[i]]
/var/folders/z5/0lnyp_m54dqc1xkz22ncbj2h0000gn/T/ipykernel_22931/4200653138.py:10: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
  plt.title(r'$\hat Y = {:.2f}+{:.2f}X$'.format(res.params[0], res.params[1]))

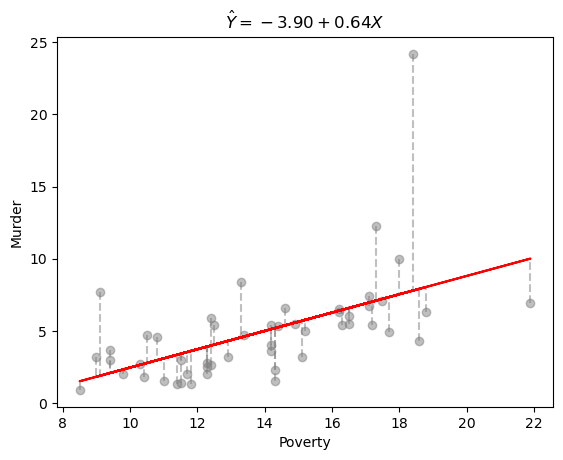
上の図で灰色のプロットは観測値で、赤い実線は推定した回帰線です。

灰色の波線は\(y_i\)と\(\hat{y_i}\)の差、残差(residual)\(\epsilon_i\)を示します。

\[\epsilon_i = Y_i - \hat{Y-i} = Y_i - \hat{\beta_1} - \hat{\beta_2}X_i\]

最小二乗法ではRSS(residual sum of squares)\(RSS=\sum_{i=1}^n\epsilon_i^2\)を最小化する\(\beta_1\)と\(\beta_2\)を推定します。