5.1. 相関・散布図

相関は、２つの量が関連して変動するかどうかを確かめるための１つの方法です。

---

分散は、

\[\frac{\sum_i(x_i-\bar{X})^2}{n} \]

でしたが、 2つの変数の方向性を示す方法として共分散があります。 共分散 ２つの変数の方向性を示す。

xとyが同じ方向に動くなら正の値、逆の方向に動く場合は負の値になります。

共分散は以下のように求められます。

\[ cov = \frac{\sum{(x_i-\bar{X})(y_i-\bar{Y})}}{n} \]

もしくは分母はn-1

---

相関係数 数値変数が互いに関連する程度を測った指標です（範囲は-1から+1）。

ピアソンの積率相関係数

\( r = \frac{\sum(x_i-\bar{X})(y_i-\bar{Y})}{\sqrt{\sum(x_i-\bar{X})^2(y_i-\bar{Y})^2}}\)

この式は、共分散（covariance）

\( cov = \frac{\sum{(x_i-\bar{X})(y_i-\bar{Y})}}{n} \)

を、xとyのそれぞれの標準偏差

\( \sigma_x = \sqrt{\frac{\sum_i(x_i-\bar{X})^2}{n}} \), \( \sigma_y = \sqrt{\frac{\sum_i(x_i-\bar{X})^2}{n}} \)

の積で割ったもの（\(r = \frac{cov}{\sigma_x\sigma_y}\)）です。

---

相関行列 行と列が変数を表し。セル値が変数間の相関関係を表す表。

---

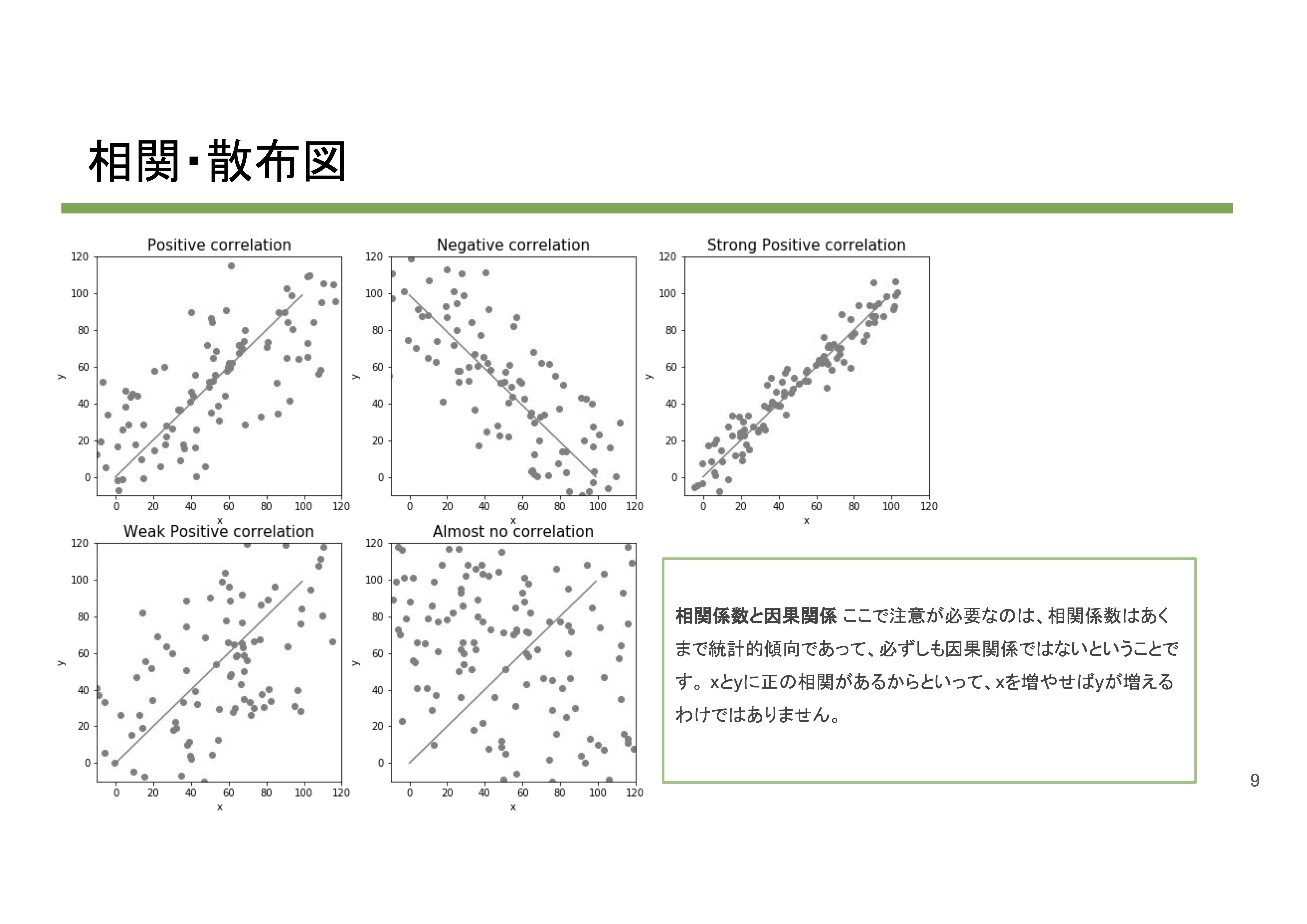
散布図 x軸に変数の値、y軸に別の変数の値をとる図。

---

相関係数と因果関係 ここで注意が必要なのは、相関係数はあくまで統計的傾向であって、必ずしも因果関係ではないということです。 xとyに正の相関があるからといって、xを増やせばyが増えるわけではありません。

---

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline

df = pd.DataFrame({'x': [10, 12, 14, 20, 25, 26, 19, 21, 17, 11, 14, 13],
                   'y' :[460, 390, 490, 610, 890, 880, 1200, 1300, 840, 620, 450, 560]})

df.describe()

	x	y
count	12.000000	12.000000
mean	16.833333	724.166667
std	5.373899	299.316140
min	10.000000	390.000000
25%	12.750000	482.500000
50%	15.500000	615.000000
75%	20.250000	882.500000
max	26.000000	1300.000000

.corr() を使ってピアソンの積立相関係数を求めます。

corr_scr = df['x'].corr(df['y'])
print('Pearson Correlation: ', corr_scr)

Pearson Correlation:  0.6764276866627554

2次元以上のDataFrameへ .corr() を使うと相関行列を示すことができます。

df[['x','y']].corr()

	x	y
x	1.000000	0.676428
y	0.676428	1.000000

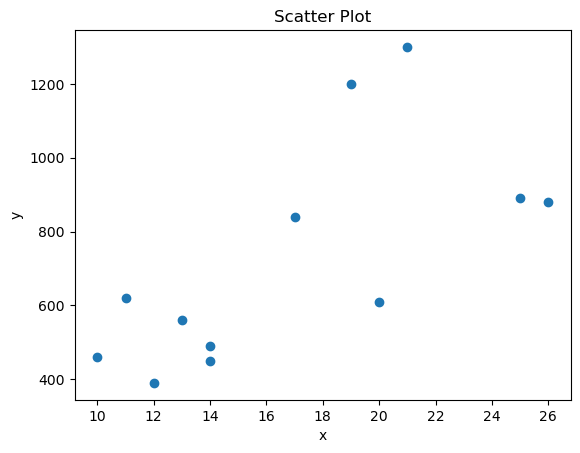
続いてMatplotlibのscatterを使って散布図を描きます。

plt.scatter(df['x'],df['y'])
plt.xlabel('x')
plt.ylabel('y')
plt.title('Scatter Plot')
plt.show()

散布図上で右上がりの直線、つまりx軸の値が増えるとy軸の値も増えるような関係（あるいはx軸が減るとy軸も減ると）を正の相関と呼びます。

右下がりの直線、つまりx軸の値が増えるとy軸の値が減っているような関係を負の相関と呼びます。

点が直線とは関係なくバラバラに散らばっている場合は相関がないとします。