6.2. 順序ロジットモデル

前節までのロジットモデルやプロビットモデルでは被説明変数が2つの値から1つを選ぶケースを扱っていました。ここでは、被説明変数が3つ以上の値から一つを選ぶ離散選択モデルを扱います。具体的には、順序ロジットモデル（orderd logit model、本頁）と多項ロジットモデル（multinomial logit model、次頁）を取り上げます。

順序ロジットモデル（ordered logt model） 順序ロジットモデルは、被説明変数が取りうる値が3つ以上、かつ、それらに何らかの順序がある場合に適用します。

Note

順序ロジスティック回帰で扱う例としては、「優れている、どちらとも言えない、劣っている」の中から1つを選ぶ場合や、公共交通機関を利用する頻度が「ほぼ毎日、週5日程度、週２-3日程度、週1日程度、ほぼない」から1つを選ぶ場合などが該当します。

例1：ある研究で、個々人がスマートフォンで位置情報を取得されることについてどのような意識を持っているかを調べています。個々人位置情報が収集されることに抵抗があるかどうか「とても当てはまる」、「どちらかというと当てはまる」、「どちらでもない」、「どちらかというと当てはまらない」、「全く当てはまらない」という5つの選択肢から選んでもらうことにしました。どのような属性（学歴・就業状況・年齢など）を持つ人ほど、その意識に当てはまりやすいのかを推定します。ここで、分析に当たっては5つの選択肢の間の「距離」が等しくないと考えます。

---

ここでは、UCLAのページ(https://stats.oarc.ucla.edu/r/dae/ordinal-logistic-regression/)で公開されている順序ロジスティック回帰の説明を参考にPythonで分析をしてみましょう。

分析例として扱うのは、大学院への進学の意思決定与える影響要因の調査です。大学3年生に、大学院に出願する可能性は低いか、やや高いか、非常に高いかを尋ねたサンプルデータを用います。この例では、被説明変数変数には3つのカテゴリーがあり、説明変数としては親の教育状況、学部が公立か私立か、現在のGPAに関するデータなどがあります。

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from statsmodels.miscmodels.ordinal_model import OrderedModel

%matplotlib inline

まずはデータをダウンロードして最初の３行を表示させてみましょう。

url = "https://stats.idre.ucla.edu/stat/data/ologit.dta"
data_student = pd.read_stata(url)

data_student.head(3)

	apply	pared	public	gpa
0	very likely	0	0	3.26
1	somewhat likely	1	0	3.21
2	unlikely	1	1	3.94

各行に調査に回答した大学生のデータが収録されています。apply列に、大学院への進学について「可能性が低い」「やや高い」「非常に高い」という回答結果が入っています。また、以下の変数が確認できます。

• pared: 少なくとも片方の親が大学院の学位を持っているかどうかを示す0/1の変数

• public: 学部が公立であれば1、私立であれば0とするダミー変数

• gpa: 学生の成績平均で0から4の間の値をとる

以下、pared, public, gpaを説明変数、applyを被説明変数とする順序ロジットモデルを考えます。

data_student.dtypes

apply     category
pared         int8
public        int8
gpa        float32
dtype: object

paredがcategoryというタイプとなっていることがわかります。

See also

pandasでのカテゴリ変数の扱いについては次のページを確認してください。 https://pandas.pydata.org/docs/user_guide/categorical.html

被説明変数applyの3つのカテゴリごとにGPAの値がgpaどのように分布しているのかを確認します

fontsize = 10
fig, ax = plt.subplots(figsize=(5,3))
target_cat = data_student['apply'].unique()
data = [data_student.loc[data_student['apply'].isin([x]),'gpa'] for x in target_cat]
ax.boxplot(data, 
            labels = target_cat,
            meanprops = {"marker": "^",
             "markerfacecolor": "red",
             "markeredgecolor": "red",
             "markersize": "8"},
            showmeans=True)
ax.set_title('Box plot of average GPA', fontsize=fontsize)
ax.set_xticklabels(ax.get_xticklabels(), fontsize=fontsize)
ax.grid()
plt.show()

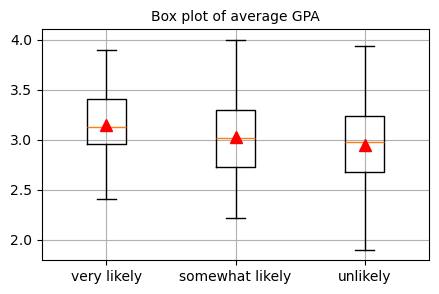
ヒストグラムでも同じデータを可視化で確認してみます

fontsize = 10
fig, ax = plt.subplots(figsize=(5,3))
ax.hist(data, label=target_cat, alpha = 0.9, color = ['#fdae61','#abdda4','#2b83ba'])
ax.legend(frameon=False, fontsize=fontsize)
ax.set_title("Histogram of average GPA", fontsize=fontsize)
plt.show()

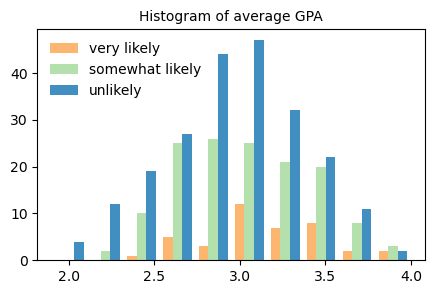
少なくとも片方の親が大学院の学位を持っているかどうかparedと学部が公立であるかどうかpublicによって、大学院への進学意思はどのように変わるのかも平均値と標準偏差から概観します・

data_student.groupby(['apply'])[['public','pared']].agg(['mean', 'std'])

/var/folders/z5/0lnyp_m54dqc1xkz22ncbj2h0000gn/T/ipykernel_22960/3682748974.py:1: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  data_student.groupby(['apply'])[['public','pared']].agg(['mean', 'std'])

	public		pared
	mean	std	mean	std
apply
unlikely	0.140909	0.348721	0.090909	0.288135
somewhat likely	0.114286	0.319300	0.214286	0.411799
very likely	0.250000	0.438529	0.325000	0.474342

\(Y_i^*\)は潜在変数で、観測された順序変数\(Y\)が何に等しいかを決定します。潜在変数\(Y^*\)はいくつかの閾値\(m_j\)を持っていて、観測された変数\(Y\)の値は、特定の閾値を超えたかどうかに依存します。例えば、\(j=5\)では、順序ロジットモデルは以下のような式となります。

\[\begin{split}Y_i = \begin{cases} 5 & \text{if} & m_5<Y_i^*\\ 4 & \text{if} & m_4<Y_i^*\leq m_5\\ 3 & \text{if} & m_3<Y_i^*\leq m_4 & \text{where } & Y^*_i=a+bX_i+u_i\\ 2 & \text{if} & m_2<Y_i^*\leq m_3\\ 1 & \text{if} & Y_i^* \leq m_2\\ \end{cases}\end{split}\]

\(m_j\)はカットオフ（cut-off）と呼ばれ、m_jより大きいか小さかでYが特定の値を取る確率を求めます。

statsmodelsを用いて推定します。

mod_logit = OrderedModel(data_student['apply'],
                        data_student[['pared', 'public', 'gpa']],
                        distr='logit')

res_logit = mod_logit.fit(method='bfgs')
print(res_logit.summary())

Optimization terminated successfully.
         Current function value: 0.896281
         Iterations: 22
         Function evaluations: 24
         Gradient evaluations: 24
                             OrderedModel Results                             
==============================================================================
Dep. Variable:                  apply   Log-Likelihood:                -358.51
Model:                   OrderedModel   AIC:                             727.0
Method:            Maximum Likelihood   BIC:                             747.0
Date:                Mon, 30 Dec 2024                                         
Time:                        08:25:00                                         
No. Observations:                 400                                         
Df Residuals:                     395                                         
Df Model:                           3                                         
===============================================================================================
                                  coef    std err          z      P>|z|      [0.025      0.975]
-----------------------------------------------------------------------------------------------
pared                           1.0476      0.266      3.942      0.000       0.527       1.569
public                         -0.0586      0.298     -0.197      0.844      -0.642       0.525
gpa                             0.6158      0.261      2.363      0.018       0.105       1.127
unlikely/somewhat likely        2.2035      0.780      2.827      0.005       0.676       3.731
somewhat likely/very likely     0.7398      0.080      9.236      0.000       0.583       0.897
===============================================================================================

上の結果で「unlikely/somewhat likely」と「somewhat likely/very likely」はカットポイントと呼ばれる切片で、3つのグループを生成するために潜在変数がどこで切断されるかを示しています。一般的にこれらの結果は結果の解釈に用いません。

オッズ比も求めます。

params = res_logit.params
conf = res_logit.conf_int()
conf['Odds Ratio'] = params
conf.columns = ['2.5%', '97.5%', 'Odds Ratio']
print(np.exp(conf))

                                 2.5%      97.5%  Odds Ratio
pared                        1.693333   4.799784    2.850901
public                       0.526033   1.690759    0.943077
gpa                          1.110697   3.085286    1.851167
unlikely/somewhat likely     1.965376  41.738049    9.057094
somewhat likely/very likely  1.791009   2.451586    2.095426

Formulaを書く方法でもOKです。

modf_logit = OrderedModel.from_formula("apply ~ 1 + pared + public + gpa", data_student,
                                      distr='logit')
resf_logit = modf_logit.fit(method='bfgs')
print(resf_logit.summary())

Optimization terminated successfully.
         Current function value: 0.896281
         Iterations: 22
         Function evaluations: 24
         Gradient evaluations: 24
                             OrderedModel Results                             
==============================================================================
Dep. Variable:                  apply   Log-Likelihood:                -358.51
Model:                   OrderedModel   AIC:                             727.0
Method:            Maximum Likelihood   BIC:                             747.0
Date:                Mon, 30 Dec 2024                                         
Time:                        08:25:00                                         
No. Observations:                 400                                         
Df Residuals:                     395                                         
Df Model:                           3                                         
===============================================================================================
                                  coef    std err          z      P>|z|      [0.025      0.975]
-----------------------------------------------------------------------------------------------
pared                           1.0476      0.266      3.942      0.000       0.527       1.569
public                         -0.0586      0.298     -0.197      0.844      -0.642       0.525
gpa                             0.6158      0.261      2.363      0.018       0.105       1.127
unlikely/somewhat likely        2.2035      0.780      2.827      0.005       0.676       3.731
somewhat likely/very likely     0.7398      0.080      9.236      0.000       0.583       0.897
===============================================================================================